Blog Archives
Open Channel Flow – Manning Equation
Manning’s Equation for open channel flow is the go-to equation for open channel problems. An open channel is basically anything that flows out in the open above ground as well as pipes that are not flowing to their full capacity.
$$ Q = \frac{1.49AR^{\frac{2}{3}}\sqrt{s}}{n} $$
Q is the flow and can be in either cubic feet per second (US) or cubic meters per second (SI). When using the equation for SI units leave out the 1.49 factor!
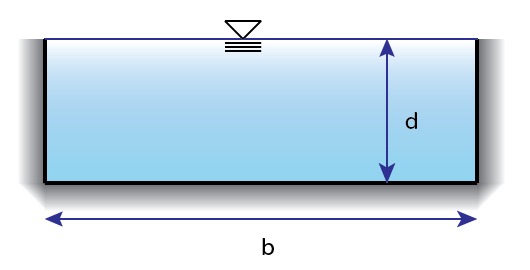
A is the Area of the channel. This can be determined with geometry for the easy rectangular and trapezoidal shapes or using table equations in combination with depth, base length, diameter etc. Find where channel geometry equations are in your reference.
Closed Conduit Hydraulics – Friction and Minor Losses
Friction and minor losses are glossed over in the darcy-weisbach article but I want to throw in some extra notes here. Friction occurs over every bit of length of a close-conduit system and is usually a surprisingly high amount of energy loss. Friction depends on the material of the pipe and the velocity of flow. The formula for frictional head loss IS the Darcy-Weisbach equation.
$$ h_f = f \frac{L}{D}\frac{V^2}{2g} $$
Closed Conduit Hydraulics – Bernoulli Equation
The Bernoulli Equation is used to analyze flow in closed pipe systems and is one of the most used equations in hydraulics (that I can remember!).
The base form of the equation relates energy between two or more points in a system. I think it is easier to remember and use in terms of head loss(ft or m).
$$ h_f = \frac{V_1^2}{2g}+\frac{p_1}{\rho g} + z_1 = \frac{V_2^2}{2g}+\frac{p_2}{\rho g} + z_2 $$ Click here to continue reading
Closed Conduit Hydraulics – Hazen Williams Equation
Hazen-Williams can be used to determine the flow characteristics in closed conduits (pipe systems).
For Velocity
$$ V = 1.318CR^{0.63}S^{0.54} \text{ (US)}$$
$$ V = 0.849CR^{0.63}S^{0.54} \text{ (SI)}$$
S = slope, in decimal form. This is equivalent to \( h_f/L\)
R = hydraulic radius, \(\text{(Area of flow)}/\text{(wetted perimeter)}\)
C = Roughness Coefficient, get this from a table (available in both the AIO and CERM) Click here to continue reading