Blog Archives
Time of Concentration
The time of concentration ($$t_c$$) is the time needed for water to flow from the farthest point in a watershed to the outlet of the watershed. Definition aside (which is taken straight from Wikipedia) there are a lot of formula’s that solve for time of concentration. So many that I doubt it’s validity in all cases and wonder if it will be on the breadth test :). Without further ado, the formula’s:
Kirpich (general, mostly rural)
$$ t_c = 0.0078L^{0.77}S^{-0.385} $$
Kirpich’s equation should be used for a lot of areas in general.
FAA Formula (Urban Areas)
$$ t_c = \frac{1.8(1.1-C)\sqrt{L}}{S^{1/3}} $$
Manning’s Kinematic Wave Formula (Paved Areas)
$$ t_c = \frac{0.938}{i^{0.4}} \left( \frac{nL_o}{\sqrt{S}} \right)^{0.6} $$
NCRS Lag Equation (Small urban areas, most cities)
$$ t_c = \frac{1.67 L_o^{0.8} \left(\frac{1000}{CN}-9 \right)^{0.7}}{1900S^{0.5}} $$
Kerby’s Equation
$$ t_c = 0.67 \left( \frac{nL_o}{ \sqrt{S} } \right)^{0.467} $$
I am not a hydrologist, so which of these to use is a shot in the dark. I think part of being a hydrologist is picking your favorite of these methods and modifying it to fit your own needs for your region.
For those of us just tackling this stuff on the breadth test, well, I am definitely taking these formulas into the test with me… will I use them? I hope not, but if I have to I will pick one of them based on what variables I am given.
Slope Stability Basics

The single biggest thing to know about slope stability, the breadth PE, is the factor of safety numbers:
1.5 – Permanent conditions
2.0 – Slope is supporting a building foundation
1.3 – temporary slope conditions
These will probably be in a word problem.
What is the factor of safety?
The factor of safety is a ratio of how stable the slope is given soil characteristics and geometry of the slope (angle and height etc).
The methods of determining the factor of safety for slope stability are somewhat advanced. I think they will definitely appear on the depth exam but likely not on the breadth. I suggest knowing they exist and where they are (Ch 210 Goswami, 40-7 CERM).
What Causes Slope Failure?
All of these things cause failure, eventually:
- Steepening of slopes
- Increase in groundwater pressure
- Weathering (which may be related to steepness)
- Vibrations, especially repetitive vibrations (traffic), or extreme vibrations (earthquakes)
- Extra Loading above the slope
- Excavation at the toe of the slope
What prevents Slope Failure?
- Making it less steep through grading
- Retaining structures
- Weight at the tow
- Less weight above the slope
- Reduce or remove vibrations
- basically reverse the causes….
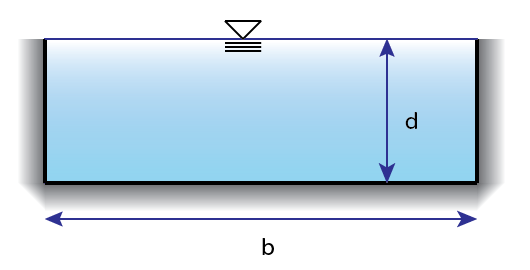
Open Channel Flow – Manning Equation
Manning’s Equation for open channel flow is the go-to equation for open channel problems. An open channel is basically anything that flows out in the open above ground as well as pipes that are not flowing to their full capacity.
$$ Q = \frac{1.49AR^{\frac{2}{3}}\sqrt{s}}{n} $$
Q is the flow and can be in either cubic feet per second (US) or cubic meters per second (SI). When using the equation for SI units leave out the 1.49 factor!
A is the Area of the channel. This can be determined with geometry for the easy rectangular and trapezoidal shapes or using table equations in combination with depth, base length, diameter etc. Find where channel geometry equations are in your reference.
Closed Conduit Hydraulics – Friction and Minor Losses
Friction and minor losses are glossed over in the darcy-weisbach article but I want to throw in some extra notes here. Friction occurs over every bit of length of a close-conduit system and is usually a surprisingly high amount of energy loss. Friction depends on the material of the pipe and the velocity of flow. The formula for frictional head loss IS the Darcy-Weisbach equation.
$$ h_f = f \frac{L}{D}\frac{V^2}{2g} $$