Blog Archives
Closed Conduit Hydraulics – Bernoulli Equation
The Bernoulli Equation is used to analyze flow in closed pipe systems and is one of the most used equations in hydraulics (that I can remember!).
The base form of the equation relates energy between two or more points in a system. I think it is easier to remember and use in terms of head loss(ft or m).
$$ h_f = \frac{V_1^2}{2g}+\frac{p_1}{\rho g} + z_1 = \frac{V_2^2}{2g}+\frac{p_2}{\rho g} + z_2 $$ Click here to continue reading
Closed Conduit Hydraulics – Hazen Williams Equation
Hazen-Williams can be used to determine the flow characteristics in closed conduits (pipe systems).
For Velocity
$$ V = 1.318CR^{0.63}S^{0.54} \text{ (US)}$$
$$ V = 0.849CR^{0.63}S^{0.54} \text{ (SI)}$$
S = slope, in decimal form. This is equivalent to \( h_f/L\)
R = hydraulic radius, \(\text{(Area of flow)}/\text{(wetted perimeter)}\)
C = Roughness Coefficient, get this from a table (available in both the AIO and CERM) Click here to continue reading
Earthwork Cut and Fill Calculations
I spent some time reviewing the earthwork sections that will appear on the construction breadth AND depth portions of the test and realized that the books are kind of confusing in their presentation of the formulas. I figured out a way that helps me to remember the formulas easily and these problems should be straightforward free points on the actual test.
First, a few definitions (these go by a lot of different names that mean the same thing).
In Situ, bank measure: soil as it is currently on-site. This is soil that has supposedly been at rest for a while. Even if it was compacted initially it has expanded gradually over to time to be at its current at-rest condition.
Bulk Size, Swell, Transport Size, Loose, Expanded, Excavated: This is soil that has been excavated and is loose. This is used to calculated the volume used while transporting or while sitting loosely in a pile. Click here to continue reading
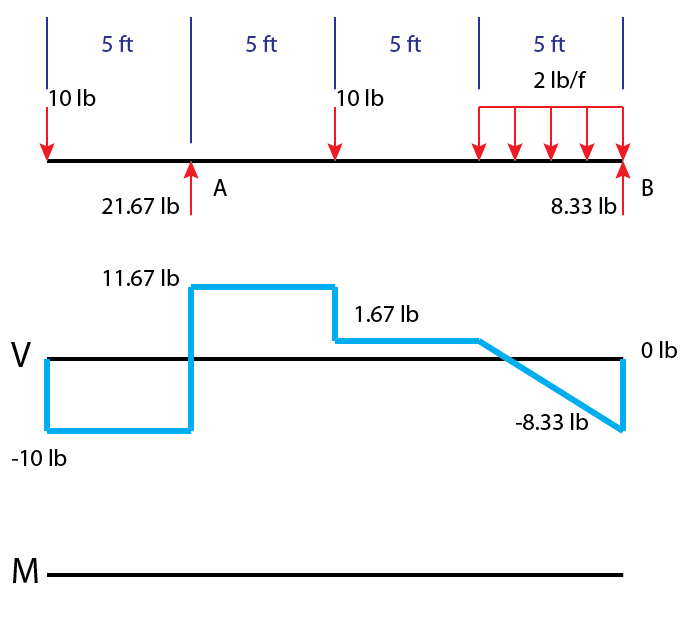
How to Draw Moment Diagrams
Moment diagrams are similar to shear diagrams, use them to find the location and value of the maximum positive and negative moment, or the moment at any specific location.
The easiest and fastest way to construct a moment-diagram is by using the areas of the regions in the shear-diagram. Before doing this you must solve for all the reactions, and solve the shear diagram.
Here is a member that is solved to the desired state to begin working on the moment diagram. The start of a moment diagram (M) is below the existing shear diagram (V).