Method of Sections

Here is a good memory refresher from Structural Analysis, the Method of Sections. Many types of problems will require this as an intermediate step so it is a good idea to become familiar with it.

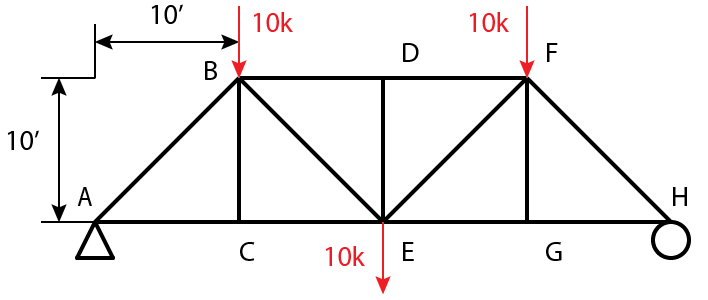
In the Frame below, Find F_BE

Member BE is in the middle of the frame here, the easiest way to find the force inside the member is to cut a section through it.

Here is how the reactions at supports A and H are calculated.

$$\sum{M_A} = 10k(10 ft) + 10k(20 ft) + 10k(30 ft) – F_{Hy}(40 ft) = 0$$

$$F_{Hy} = \frac{(100 + 200 + 300) kip ft}{40 ft} = 15k$$

$$\sum{F_y} = -10k -10k-10k + F_{Ay} + 15k = 0 $$

$$F_{Ay} = 30k – 15k = 15k$$

Speed Note: Since this shape and the forces are symmetric, \(F_{Ay}\) and \(F_{Hy}\) are equal to each other. They can be quickly calculated as half the total of the downward forces, \(\frac{10k +10k+10k}{2}=15k\).

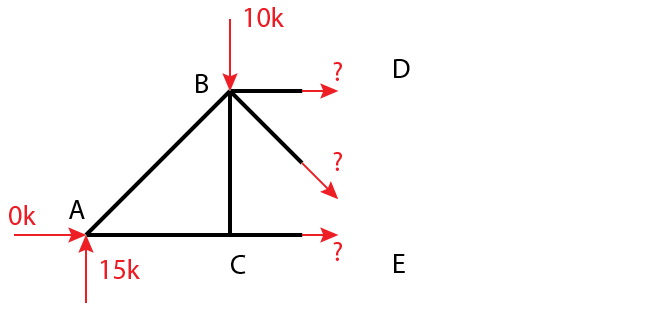
The cut left you with three unknown values that you must solve for or find a way to cancel out. There are a three paths to choose from: Sum horizontal forces, sum the vertical forces, or sum the moments about a point. The one that should be the fastest is summing the vertical forces as the only unknown vertical force is a component of \(F_{BE}\).

$$\sum{F_y} = 15k – 10k – \frac{1}{\sqrt{2}}*F_{BE} = 0$$

$$ F_{BE} = (15k – 10k)*\frac{\sqrt{2}}{1} \approx 7.1 k (Tension)$$

Tension was assumed initially in the drawing and since the answer came out positive the force in the member is confirmed to be in tension.

Wheeew! This is the first concept I have made notes for, this one took a while but hopefully it will be faster after a few. My books have not arrived yet so this is just representing me going through some old study material I have around the house. Enjoy!