Method of Joints
When analyzing a joint you will solve for the forces in all of the members connected to it.
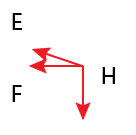
Lets start with H, draw the two unknown forces \(F_{HE}\) and \(F_{HF}\) in tension (away from H).
You already know the downward force is \(5k\). \(F_{HE}\) is the only member with a vertical component so you can solve for it.
$$\sum{F_y} = \frac{10}{\sqrt{1000}}F_{HE} – 5k=0$$
$$ F_{HE} = 5k\frac{\sqrt{1000}}{10}\approx 15.8k (Tension)$$
Ok so you know \(F_{HE}\). Use the horizontal component of \(F_{HE}\) to solve for \(F_{HF}\):
$$\sum{F_x} = -\frac{30}{\sqrt{1000}}F_{HE} – F_{HF} = 0$$
$$ F_{HF} = -\frac{30}{\sqrt{1000}} 15.8k \approx -15k (Tension) = 15k (Compression) $$
Note: \(\frac{10}{\sqrt{1000}}\) is from the geometry of the structure. \(\sqrt{1000} = \sqrt{10^2 + 30^2}\) and \(\frac{10}{\sqrt{1000}} = \sin\theta\) (where \(\theta\) is the angle of the pointy end).
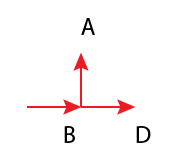
Jumping over to B
You do not know any of these forces. \(F_{BA}\) is a doozy though. Summing the vertical forces reveals that..
$$ \sum{F_y} = F_{BA} = 0$$
\(F_{BA}\) is zero. You can calculate the horizontal reaction at B by taking moments of the entire truss at A.
$$\sum{M_A} = 10k(10ft) + 10k(20ft) + 10k(30ft) – 10ft(R_{Bx}) = 0$$
$$ R_{Bx} = \dfrac{(100 + 200 + 300)k*ft}{10 ft} =60k$$
Now sum the horizontal forces to find \(F_{BD}\)
$$ \sum{F_x} = 60k + F_{BD} = 0$$
$$ F_{BD} = -60k (Tension) = 60k (Compression)$$
Sliding on over to D
At this joint we know that \(F_{DB} = 60k( Compression)\) (so the arrow should actually point inward for compression), and that the downward force is 5k. We have three unknowns and only two equations (\(\sum{F_x}\) and \(\sum{F_y}\)). This joint is unsolvable so you must move on to another joint before coming back to it.
After practice you start to see the paths to take. At this point E is solvable (secret zero-force member), and then F will be solvable, and then D would be too.
Combining the Method of Joints with the Method of Sections makes things even faster because you can often jump straight to a joint or area that you need for the problem (it may only ask you to find one member for example).
Posted in Structural Breadth and tagged frame, mechanics, method of joints, pe exam, structural. Bookmark the permalink. Leave a Comment.




Leave a Comment
Comments (0)