How to Solve for Reactions

The first step in many problems is solving for reactions, here is an example of some situations that you may encounter.

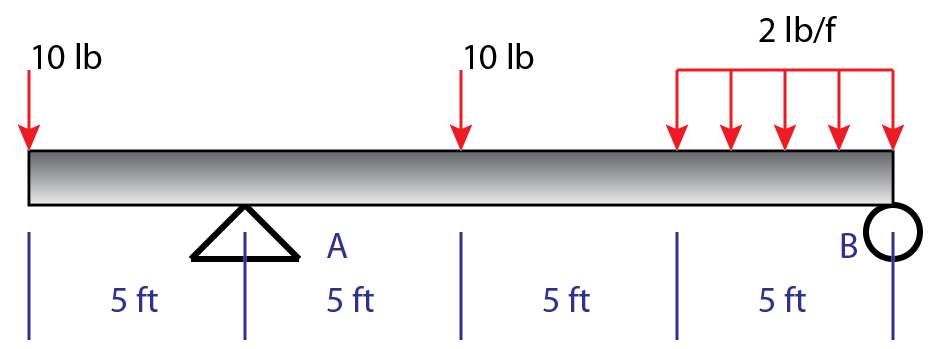
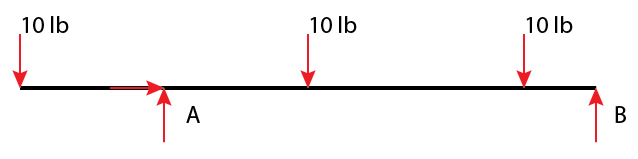
Simplify the distributed load into a point load:

$$ \frac{2lb}{ft} *5ft = 10 lb $$

Since this distribution is constant the load is applied at the midpoint, 2.5 ft to the left of B. (If the distributed load was not linear the point load should be applied at wherever the “center of mass” of the distributed load is; the center of mass of a constant distributed load is the midpoint).

Now you can continue on to finding the reactions:

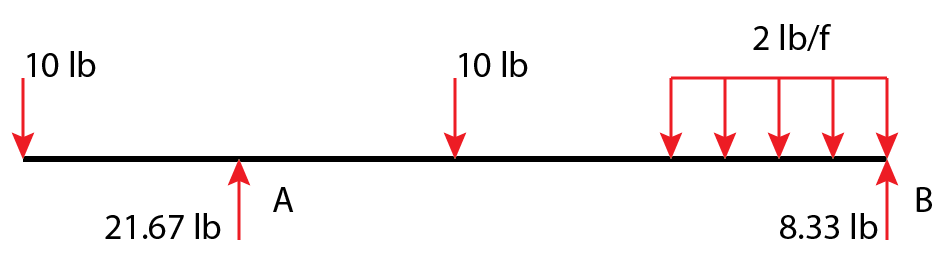
$$ \sum{M_A} =  10 lb (5ft) – 10lb(5ft) – 10lb(12.5 ft) + F_{By} (15ft) = 0 $$

$$ F_{By} = \frac{-50 + 10 +  125}{15} = 8.33 lb $$

$$ \sum{F_y} = -10 + F_{Ay} – 10 – 10 + 8.33 = 0$$

$$  F_{Ay} = 10 + 10 + 10 – 8.33 = 21.67 lb $$

$$ \sum{F_x} = F_{Ax} = 0 $$