Blog Archives
Rainfall Intensity Analysis
The intensity (I or i) of a rainfall event is a storm characteristic that measures the rainfall rate. In America this is in inches per hour ( $$\dfrac{in}{hr}$$ ).
I think the primary reason to determine the intensity is for use in the rational method of determining peak storm flow.
The two main methods I have found to get the intensity are from Intensity-Duration-Frequency (IDF) Curves and from empirical formulas (Steel Equation).
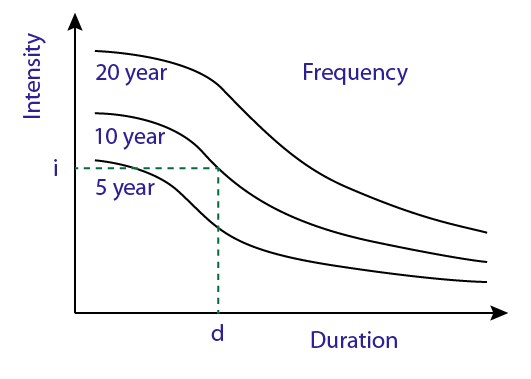
IDF Curve
IDF Curves are curves that have been put together for a specific region using multiple years (decades) of recorded storm data. Here is an example.
To get intensity, you need to know the storm frequency as well as the storm duration. If the storm frequency is not one of the common ones (5, 10, 15, 20, 50 etc) you may have to interpolate on the graph and give your best estimate. The duration also may need to be interpolated.
With the above pictured IDF Curve (which is for some place in ReviewCivilPE land), a 10 year storm that lasts for d minutes would correspond to an intensity, i. Easy!
Steel’s Formula
$$ I = \frac{K}{t_c+b} $$
The steel equation is an empirical equation for for estimating intensity and requires knowing the time of concentration (another process). You also need to determine values of the coefficients c and b (I can’t seem to find names for these at the moment).
Both the CERM and AIO provide a map of the United States divided up into geographic regions for use with Steel’s formula, and an accompanying table of c and b values.
- Find your region
- Find your return period (storm frequency)
- Get c and b values
- Success
With your time of concentration and c and b values, the Steel formula can be solved and your intensity obtained for use in the ration method.
When to Choose IDF or Steel Formula
Ah the golden question, what are the indicators of going with one method or the other? If you are given an IDF curve, and the frequency and duration I think this is a no-brainer, get it from the IDF curve!
If you are given a city or region, but no IDF curve, then you should probably shoot for the Steel Formula, they had better given you enough info to also calculate the time of concentration.
Rational Method for Peak Flow
The rational method determines the max flow (Q) at a point after a storm event.
$$ Q = CiA $$
Q, peak flow
C, runoff coefficient
i, storm intensity ($$\frac{in}{hr} $$)
A, area (acres)
To use the rational method you need to divide the watershed (area contributing flow to the point) up into separate areas depending on the runoff coefficients (C). The runoff coefficient changes based on different land types such as concrete, bare earch, turf meadow, residential etc. If the entire area is under one runoff coefficient then lucky you. If not, determine the area of each subregion and it’s accompanying C value. Tables for C values are provided in both the AIO and CERM.
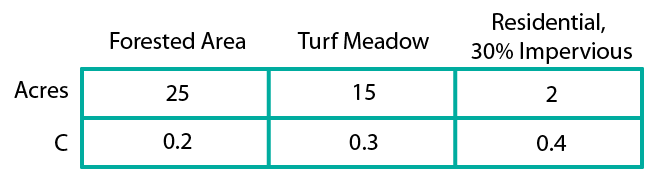
You should end up with (or be given) data similar to this:
Get the Average Runoff Coefficient
You can only enter one C value into the equation. It should be the weighted average of all of the C values.
$$ C_{avg} = \frac{ \sum{CA}}{ \sum{A} } $$
With the data above this would be:
$$ C_{avg} = \frac{25*0.2 + 15*0.3 + 2*0.4}{25+15+2} = 0.245$$
On a short question like on the breadth, I am thinking that the intensity MAY be provided to you, it is sort of a process to get it on your own. Either way, get the intensity. Once you have all three values, multiply for max Q!
Let’s just say I solved for intensity (using information that has not been provided in this example) and it is 1.25 $$\frac{in}{hr}$$ (on the less-intense end):
$$ Q = C_{avg} * i * A $$
$$ Q = 1.25 * 0.245 * 42 $$
$$ Q = 12.875 \frac{ft^3}{s}$$
There you have it! This seems like a high flow to me, but it’s a huge area. And it’s an example problem, I made all these values up.
Speed Tip
You may have noticed that to solve for the $$C_{avg}$$ value you have to divide by the total area. Why would you divide by the total area to get that and then turn around and multiply by the total area when you solve or Q?
To save some time, just multiply the sum of the region areas and coefficients by the intensity. It could be rewritten as $$Q=\left( \sum{ CA_{region} }\right)*i$$.