Blog Archives
Acceleration and Deceleration
Acceleration is measured in velocity change per second, so miles per hour per second (mphps), feet per second per second (fpsps or fps/s) etc. Deceleration is negative acceleration, so I probably won’t use that term from here on out and simply stitch with acceleration.
If you are starting from zero with an acceleration of 3 fps/s, your velocity will increase by 3 for every second from then on. So 0, 3, 6, 9, 12 etc.
There is one equation relating velocity(v) and acceleration(a):
$$ v_f = v_0 + at$$
Use this equation for any problem with initial and final velocity, and acceleration. Click here to continue reading
Stopping Sight Distance
The stopping sight distance (SSD) is the total distance you travel during the time you (a) react to apply brakes, (b) apply brakes and actually begin to decelerate, and (c) vehicle comes to a stop.
Reaction time from AASHTO (\( t_R\)) is 2.5 s.
Default deceleration rate from AASHTO is 11.2 \(ft/s^2\)
The total distance traveled using these values on a straight path is:
$$ SSD = Vt_R + \frac{V^2}{2(a\mp gG)}$$
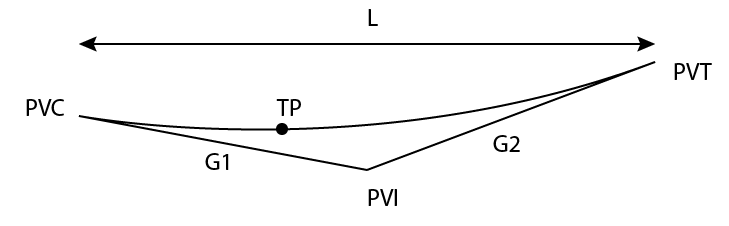
Vertical Curves
Vertical Curves are nice! I think they are easier to solve than Horizontal Curves because they are essentially parabola equations (which you should be very used to). This is the formula for vertical curves
$$ y(x) = y_{PVC} + G_1x + \frac{1}{2}Rx^2 $$
\(y(x)\) is the elevation y at x horizontal distance into the curve from the start position
\(y_{PVC}\) is the starting elevation at x = 0.
Horizontal Curves Definitions and Formulas
Horizontal Curve Formulas
$$L = 100\frac{I^{\circ}}{D^{\circ}}$$
$$L = RI_{\text{radians}}$$
$$L = \frac{RI 2 \pi}{360^{\circ}}$$
$$ R = \frac{5729.578}{D}$$
$$ T = R\tan\frac{I}{2}$$
$$ LC = 2R\sin\frac{I}{2}$$
$$ E = T\tan\frac{I}{4}$$
$$ M = E\cos\frac{I}{2}$$