Lateral Earth Pressure
Lateral Earth Pressure is the horizontal pressure applied by or to soil when it is against standing structures like basements (buildings) and retaining walls. The lateral earth pressure (\( \sigma_h’ \)) at any depth is a factor (K) of the vertical effective stress (\( \sigma_v’ \)) and cohesion (c):
Active: $$ \sigma_h’ = K_a \sigma_v’ – 2c \sqrt{K_a}$$
Passive: $$ \sigma_h’ = K_a \sigma_v’ + 2c \sqrt{K_p}$$
At Rest: $$ \sigma_h’ = K_o \sigma_v’$$
The vertical effective stress is solved for from the soil unit weight and depth of the structure.
The cohesion is usually given, and is often zero for sands or if the problem states cohesionless soil. Cohesion is the “stickiness” of the soil.
I think it is worth noting that after you determine the lateral earth pressure to use, and determine its magnitude, you can use the distributed load it gives to solve for the stability of the structure, but I will go over some notes on that in a separate post.
Types of Lateral Earth Pressure and the (simplified) equations for their coefficients (K)
I am using the simplified because I think the breadth problems will always deal with vertical structures, with flat backfill above the retaining structure, and assumed that structure is frictionless against the soil. The equation is too large otherwise.
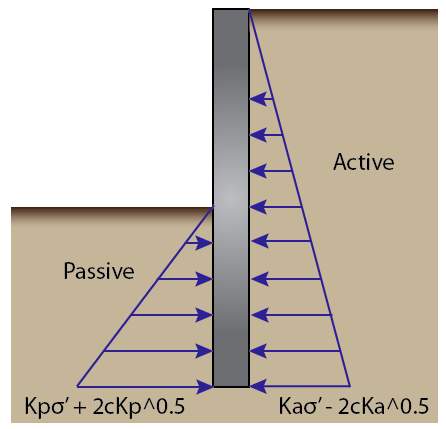
Active Earth Pressure is soil pressure that is trying to move the structure, almost all forms of earth pressure situations involve active earth pressure. The soil inducing the active pressure is breaking away from another body of soil (eg the soil behind a retaining wall would usually break away and crumble) and is in tension. The active earth coefficient is smaller than the passive one, values are typically 0.2 to 0.5. This is Rankine’s active earth pressure formula for a vertical structure with cohesion assumed to be zero (most cases):
$$ K_a = \tan ^2 \left( 45 – \frac{\phi}{2}\right ) = \frac{1-\sin \phi}{1+ \sin \phi }$$
Passive Earth Pressure is the pressure that is trying to keep the structure in place. The soil inducing the Passive pressure is under compression. The passive pressure is typically higher than the active pressure, with values in the 2 to 5 range.This is the same formula from above except for passive earth pressure (notice the small difference?):
$$ K_a = \tan ^2 \left(45 + \frac{\phi}{2} \right) = \frac{1 + \sin \phi }{1 – \sin \phi}$$
The At-Rest Soil Pressure is an assumed state where the soil and the structure are assumed to NEVER move. Think about an aircraft-carrier in the ocean, it hardly moves when it is hit by small waves. Structures like massive bridge abutments and foundations extending to bedrock are assumed to never move (or it is negligible) and the at-rest equation can be used. The values for the coefficient are slightly higher than the active but less than passive, 0.4 to 0.8 or so.
$$ K_o \approx 1 – \sin \phi$$
\(\phi \)is the friction angle of the soil. This is either given to you in the problem prompt or you have to use an assumption based on the soil type. Most references have a table with some safely assumed vales for different soil types.
What if the structure is not vertical or the backfill is not horizontal?
If the structure is not vertical you must use the expanded form of Rankine’s formula, or the Coulomb formula. Both of which are much larger and have extra variables to account for the backfill angle from horizontal (\(\beta\)) and the angle of the face of the structure from horizontal (\(lambda\)). I seriously doubt this will be on the breadth portion of the exam, so someday if somebody requests it I may add it to a geotechnical depth article.
Some notes:
- The cohesion is subtracted in the active state because the cohesion in the soil is lessening the tension forces of the active pressure (soil is trying to break away and cohesion is keeping it in place).
- Similarly the cohesion is added in the passive state because it aids in compression.
- Take note of the picture at the top that the active pressure builds up slower then than the passive pressure, this is because the coefficient of passive pressure is quite a bit higher then the coefficient for active (think of it as slope). Also please don’t pay any attention to scale in that picture.
And finally, here are some examples of when the soil pressure is active vs passive:
Active – Soil being held back by a retaining wall (the soil is trying to knock the wall over!)
Passive – Soil holding the base of a retaining wall in place (the soils is being compressed!)
Passive – Soil on the other side of a full water-reservoir tank. The water in the tank is exerting a pressure on the soil, the soil is holding it in place.
At-Rest – The soil against one of the abutments at the Golden Gate Bridge (it ain’t moving)
This is a longer topic and probably confusing so please ask questions and I will do my best to give good feedback.
Posted in Geotechnical Breadth and tagged active pressure, lateral earth pressure, passive pressure, soil mechanics. Bookmark the permalink. Leave a Comment.


Leave a Comment
Comments (0)